General Alignment Background
Multiple sequence alignment (MSA) is a crucial first step for most methods of phylogenetic estimation or model-based inference of evolutionary processes. The goal of MSA is to introduce gaps into sequences so that columns of an aligned matrix contain character states that are homologous.
This statement of homology means that if two sequences both have a residue at a position in the alignment, then a residue existed in their most recent common ancestor. This site was inherited by the descendant lineages (possibly with substitutions occurring) down to the present, observed sequences. Note that if two sequences both have gap at a position, this does not mean that their ancestor had no residue at that site - multiple deletion events are possible.
Homology is a historical property that cannot be directly observed. However, homology can be inferred by MSA methods. Generally, a MSA algorithm attempts to produce homologous alignments by scoring many plausible alignments and choosing one with the best score. Aligning two positions that display the same nucleotide (or amino acid) improves the score. Aligning two positions that are not the same decrease the score. How much of a decrease (the cost) depends on what specific substitution is implied. For example, Leucine to Isoleucine substitutions are common and would not cost much. But Cysteine to Glycine changes are rare. Therefore, aligning a Cysteine to a Glycine results in a higher penalty to the score of the alignment. Placing gaps in a sequence is penalized too. Introducing a new gap usually has a higher cost than extending an existing gap. For example, a gap open cost will be -5 while an extension cost -2, to reflect a scientist’s general belief that one longer indel event is more expected than two shorter indel events.
Most default scoring options for alignment programs are designed to balance expectations of getting similar residues in the same column and allowing for gaps. Try scoring the following alignments yourself, do you get the same answers?
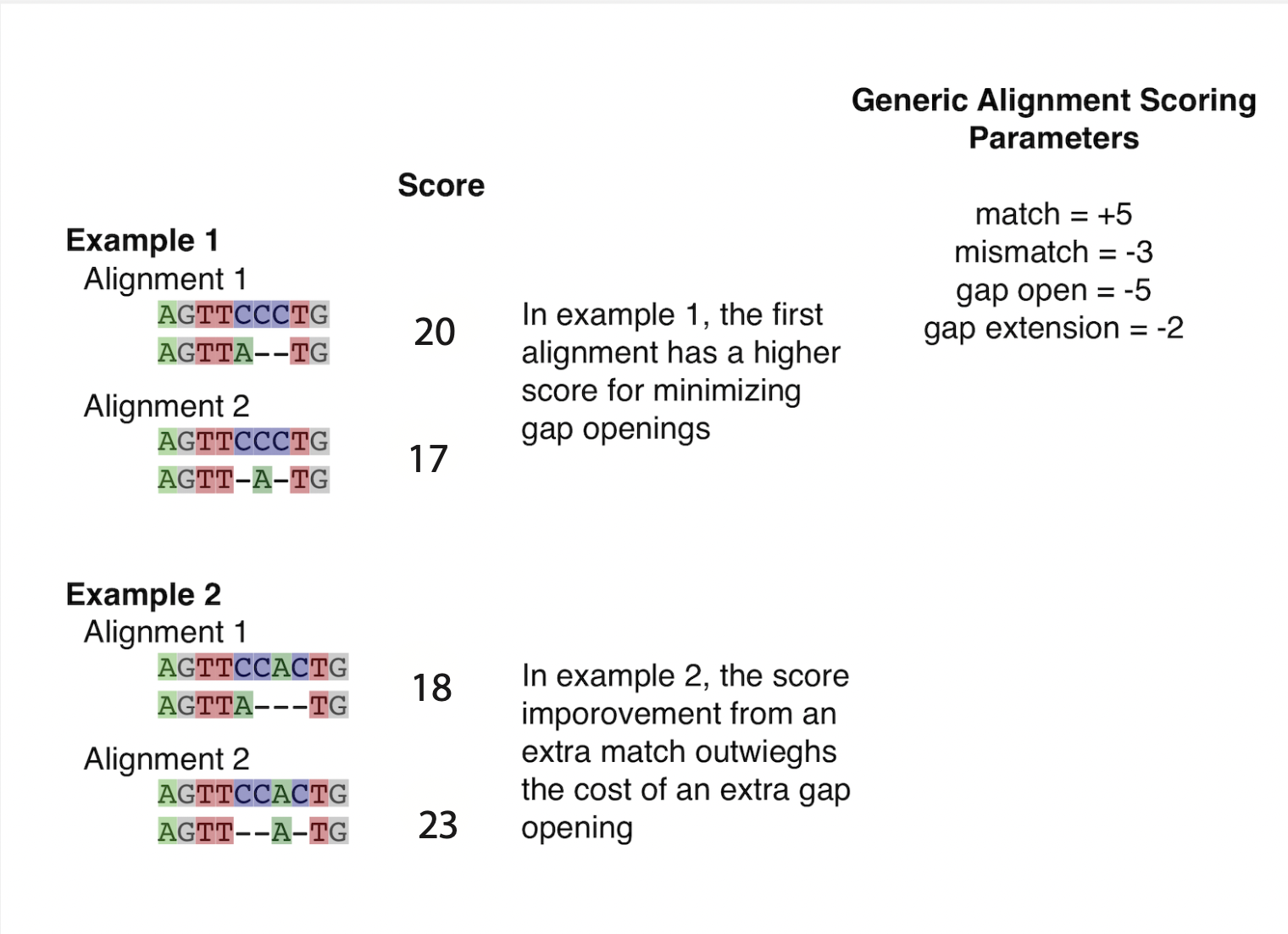
As mentioned in lecture, pairwise alignment is analytically tractable (though slow for very long sequences). Multiple sequence alignment presents new challenges:
- we do not know the evolutionary tree relating the sequences
- we do not know the states at internal nodes of the tree in the absence of data from the ancestral sequences.
Challenge 1 is frequently addressed by the use of a guide tree, but challenge 2 is for most impossible to overcome and it is not clear how the penalty terms should be applied when we align sets of more than two species. Many MSA approaches focus on solving challenge 2 in a computationally efficient way.
One common solution (and the solution used by the software we’ll talk about in this lab) is progressive alignment. The general strategy is:
- estimate pairwise distances using pairwise alignment,
- estimate a guide tree from these distances,
- use the guide tree to specify the order in which multiple sequence alignments are constructed. The algorithm proceeds by traversing the tree from leaves to the root. The two descendants of each internal node in the tree are aligned to each other. Thus, the guide tree serves as means of ordering a set of pairwise alignment operations.
- iterate until the alignment cannot be improved based on some criterion
The initial step in the progressive stage will be a pairwise sequence alignment to produce a group of two aligned sequences. But, as we move deeper in the tree, the approach will require aligning other single sequences to the previously aligned groups or aligning two distinct groups to each other (group-to-group alignment).
The score of each alignment decision during progressive alignment is usually computed using a weighted sum-of-pairs score which produces an average cost for the position in the alignment. This score reflects the costs associated with aligning each member of one descendant group to each member of the other descendant group. Another way to score an alignment of two groups is to use a consistency-based objective function that reflects how well the positions in the resulting MSA reflect the homology statements inferred from pairwise alignments (Notredame et al 1998). One of the programs we will use today, MAFFT, uses progressive alignment, but then refines the MSA with consistency.